Lets introduce some notations for talking about functions. Since a computer program has to be thought separately from the mathematical or real life objects, we must name those program procedures, they’re largely functions, and call them methods. These methods are functional in the sense that their definition and evaluation cause no side effects. Let the identity brane 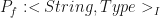 be the association of types with a set of formal parameter names:
be the association of types with a set of formal parameter names:
{
"first parameter" : Integer
"second parameter" : Boolean
}
The actual parameters, also known as the bindings for these parameters, are typed using $P_f$, the set of possible actual parameters are all dependently typed I-Brane  having instances that look like:
having instances that look like:
{
"first parameter" : 1
"second parameter" : False
}
For convenience, we endow  and members of
and members of  with mutators: for some
with mutators: for some  we can write
we can write  to mean adding a parameter to the formal parameter specification,
to mean adding a parameter to the formal parameter specification, ![P_{f-["\textrm{first parameter}"]}](https://s0.wp.com/latex.php?latex=P_%7Bf-%5B%22%5Ctextrm%7Bfirst+parameter%7D%22%5D%7D&bg=ffffff&fg=111111&s=0&c=20201002) to mean removing a formal parameter. similarly: with
to mean removing a formal parameter. similarly: with  the expression
the expression ![p_{[-"\textrm{first paramter}"]}](https://s0.wp.com/latex.php?latex=p_%7B%5B-%22%5Ctextrm%7Bfirst+paramter%7D%22%5D%7D&bg=ffffff&fg=111111&s=0&c=20201002) has type
has type ![P_{f-["\textrm{first parameter}"]}](https://s0.wp.com/latex.php?latex=P_%7Bf-%5B%22%5Ctextrm%7Bfirst+parameter%7D%22%5D%7D&bg=ffffff&fg=111111&s=0&c=20201002) belowing to the set of possible parameters
belowing to the set of possible parameters ![P_{a-["\textrm{first parameter}"]}](https://s0.wp.com/latex.php?latex=P_%7Ba-%5B%22%5Ctextrm%7Bfirst+parameter%7D%22%5D%7D&bg=ffffff&fg=111111&s=0&c=20201002) and can be used in the full invocation of any method typed
and can be used in the full invocation of any method typed ![P_{f-["\textrm{first parameter}"]}\rightarrow\Psi](https://s0.wp.com/latex.php?latex=P_%7Bf-%5B%22%5Ctextrm%7Bfirst+parameter%7D%22%5D%7D%5Crightarrow%5CPsi&bg=ffffff&fg=111111&s=0&c=20201002) Invocation on underspecified parameters automatically curries: applying
Invocation on underspecified parameters automatically curries: applying  to a underspecified parameter
to a underspecified parameter  (here,
(here,  is a collection of parameters missing
is a collection of parameters missing  ) then
) then  .
.
Finally we type the type signature for the method differential:

Note the 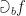 should mostly be defined for methods
should mostly be defined for methods  that has
that has 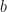 as a formal parameter:
as a formal parameter:  .
.
Now then, a method  has a formal parameter
has a formal parameter  that is of interest. To evaluate the differential of
that is of interest. To evaluate the differential of 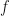 with respect to
with respect to 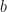 , we assert that at any parameter of
, we assert that at any parameter of 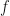
![p'\in P_{f-[b]}](https://s0.wp.com/latex.php?latex=p%27%5Cin+P_%7Bf-%5Bb%5D%7D&bg=ffffff&fg=111111&s=0&c=20201002) , the application of differential to a change in the parameter
, the application of differential to a change in the parameter 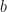 (
( ) from
) from 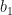 to
to  results in the proper change in the output of
results in the proper change in the output of 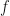 itself.
itself.

Analogously, we have converted the multiplication  of
of  to a method
to a method  and evaluated it at
and evaluated it at  to produce
to produce  . This conversion is quite native to computer programs. Since there is not a universal way to properly write
. This conversion is quite native to computer programs. Since there is not a universal way to properly write  for all possible
for all possible  as we have in mathematical language, the solution is to encode the change in the form of methods.
as we have in mathematical language, the solution is to encode the change in the form of methods.
Technically, if we encode changes as methods, the full blown differential has type:

And the equal expression of meaning, assuming  , will be:
, will be:

Finally, we introduce a factored version of the program differential:
![\Game_{\delta b}: \big(P_f\rightarrow\Psi\big)\rightarrow P_{f-[b]}\rightarrow B\rightarrow B\rightarrow\Psi\rightarrow\Psi](https://s0.wp.com/latex.php?latex=%5CGame_%7B%5Cdelta+b%7D%3A+%5Cbig%28P_f%5Crightarrow%5CPsi%5Cbig%29%5Crightarrow+P_%7Bf-%5Bb%5D%7D%5Crightarrow+B%5Crightarrow+B%5Crightarrow%5CPsi%5Crightarrow%5CPsi&bg=ffffff&fg=111111&s=0&c=20201002)
Requiring that

We may use any of these three as they becomes more convenient.
Constant and Order of Differential
An interesting idea to explore based on this differential is the order of dependence of a function on a parameter. If a method does not depend on a variable, its differential would be the identity function 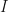 :
:

This is  . But there are also first order terms who has constant,
. But there are also first order terms who has constant,  , differential
, differential  . In this case we can find an equivalent method typed as:
. In this case we can find an equivalent method typed as:
 (*)
(*)
Where

That it does not depend on any input variables. And certainly there is something resembling  , with constant
, with constant  :
:

Our 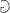 allows for arbitrarily complex changes in output value even when the input parameter changes are not small. Methods with thusly typed differentials do more than constant functions but are not as dependent on its inputs than functions with non-constant differentials. We are therefore inspired to qualify or even quantify the complexity of dependence a method has on its parameter. It is the complexity of the differential function.
allows for arbitrarily complex changes in output value even when the input parameter changes are not small. Methods with thusly typed differentials do more than constant functions but are not as dependent on its inputs than functions with non-constant differentials. We are therefore inspired to qualify or even quantify the complexity of dependence a method has on its parameter. It is the complexity of the differential function.
(*) here, the  means, essentially, or for all intents and purposes, the same. This seems like an important idea to formalize, perhaps in a next step of this effort.
means, essentially, or for all intents and purposes, the same. This seems like an important idea to formalize, perhaps in a next step of this effort.
Chain Rule
Relatedly, the simple treatment of composition and curried methods  is to uncurry them to an essentially equivalent method
is to uncurry them to an essentially equivalent method  before computing differential. The actual implementation of that differential can be programmed using the chain rule. For this composition of methods:
before computing differential. The actual implementation of that differential can be programmed using the chain rule. For this composition of methods:
![z\left(\left\{p_f:P_f, p'_g:P_{g-[x]}, x:X\right\}\right)=f\left(p_f+\left\{y:g\left(p'_g+\{x:x\}\right)\right\}\right)](https://s0.wp.com/latex.php?latex=z%5Cleft%28%5Cleft%5C%7Bp_f%3AP_f%2C+p%27_g%3AP_%7Bg-%5Bx%5D%7D%2C+x%3AX%5Cright%5C%7D%5Cright%29%3Df%5Cleft%28p_f%2B%5Cleft%5C%7By%3Ag%5Cleft%28p%27_g%2B%5C%7Bx%3Ax%5C%7D%5Cright%29%5Cright%5C%7D%5Cright%29&bg=ffffff&fg=111111&s=0&c=20201002)
And we’d like to compute  . After juggling the types and parameters a bit one discovers that the differential can be written directly as the method:
. After juggling the types and parameters a bit one discovers that the differential can be written directly as the method:

This, then, is the chain rule for program differentials.
Todo: write the proof for this chain rule.
The Limit
The reality of the matter is that the program differential  is not quite the equivalent of partial differentiation over real functions. There inside the definition of derivative is a limit. If we could take the limit of programming objects, then we can actually come to a equally localized derivative as we have for real functions. Instead of a limit
is not quite the equivalent of partial differentiation over real functions. There inside the definition of derivative is a limit. If we could take the limit of programming objects, then we can actually come to a equally localized derivative as we have for real functions. Instead of a limit  the program form of the partial differentiation would ask for:
the program form of the partial differentiation would ask for:


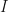 is the identity meaning no change. But that is perhaps work for another entry, to iron those details of program limits. We may yet achieve a unified world where mathematical differentiation is a sub-type of program differentiation:
is the identity meaning no change. But that is perhaps work for another entry, to iron those details of program limits. We may yet achieve a unified world where mathematical differentiation is a sub-type of program differentiation:
